Infopunkt: Flächeninhalt
Die Größe von Flächen
Tina und Max zeichnen jeweils ein Rechteck auf Kästchenpapier.
Max behauptet sein Rechteck hätte eine größere Fläche als das von Tina, Tina behauptet das Gegenteil.
Wer hat recht? Wie kann die Fläche bestimmt werden?
Die Größe einer Fläche wird als Flächeninhalt bezeichnet.
Den Flächeninhalt verschiedener Flächen kann man durch „auslegen“ mit Einheitsflächen vergleichen.
Zählt man die Kästchen der beiden Rechtecke von Tina und Max, stellt man fest, dass sich beide mit 18 Kästchen auslegen lassen.
Beide Rechtecke sind also gleich groß und haben einen Flächeninhalt von 18 Kästchen.
Einheiten des Flächeninhalts
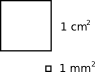Nicht immer eignen sich die Kästchen in deinem Heft zur Bestimmung von Flächeninhalten. Für sehr kleine oder große Flächen werden unterschiedliche Einheitsquadrate verwendet. Typisch sind zum Beispiel:
| Einheitsquadrat mit | Name der Einheit | Zeichen | Flächeninhalt | zur Angabe der Größe von |
| 1 mm Seitenlänge | Quadratmillimeter | mm2 | 1 mm2 | |
| 1 cm Seitenlänge | Quadratzentimeter | cm2 | 1 cm2 = 100 mm2 | Briefmarken |
| 1 dm Seitenlänge | Quadratdezimeter | dm2 | 1 dm2 = 100 cm2 | einer A4-Seite |
| 1 m Seitenlänge | Quadratmeter | m2 | 1 m2 = 100 dm2 | Wohnzimmern |
| 10 m Seitenlänge | Ar | a | 1 a = 100 m2 | Volleyballfeldern |
| 100 m Seitenlänge | Hektar | ha | 1 ha = 100 a | Fußballfeldern |
| 1 km Seitenlänge | Quadratkilometer | km2 | 1 km2 = 100 ha | Bundesländern |
Beispiel 1
Der Flächeninhalt diesen Rechtecks beträgt 4 cm2. Jedes einzelne Quadrat ist 1 cm2 groß.
Aber auch diese Figuren haben einen Flächeninhalt von 4 cm2:
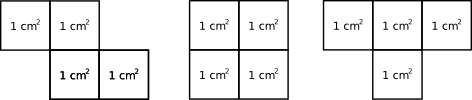
Flächeninhalte berechnen
Max hat ein Rechteck mit 7 cm Länge und 4 cm Breite gezeichnet und darin Einheits-quadrate mit 1 cm Seitenlänge zum Auszählen des Flächeninhalts eingezeichnet.
Tina sagt: „Hey Max, da sind ja in jeder der 4 Reihen 7 Quadrate - da brauchst du doch gar nicht alle Kästchen zählen!“
Was meint Tina? Kann Max den Flächeninhalt auch ohne Auszählen bestimmen?
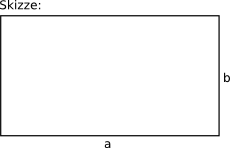
Der Flächeninhalt A eines Rechtecks ist das Produkt von Länge und Breite.
A = a · b
Mit dieser Formel kann Max nun den Flächeninhalt ausrechnen:
A = a · b
A = 7 cm · 4 cm
A = 28 cm2
Der Flächeninhalt des Rechtecks beträgt 28 cm2.
Beispiel 2
Bauer Lindemann möchte gern wissen, wie viel Weidefläche seine 2 Ziegen auf der 60 m langen und 30 m breiten Weidefläche abgrasen können.
Gesucht:
Flächeninhalt A
Gegeben:
a = 60 m; b = 30m
Rechnung:
A = a · b
A = 60 m · 30 m
A = 1800 m2
Die Weidefläche beträgt 1800 m2.
Flächeninhalt von Quadraten
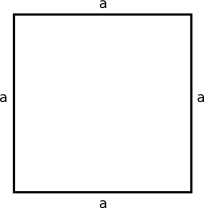Du weisst, dass Quadrate spezielle Rechtecke sind. Alle Seiten sind gleich lang. Somit vereinfacht sich die Formel zur Flächeninhaltsbestimmung:
A = a · a
Der Flächeninhalt A eines Quadrats ist das Produkt der Seitenlänge mit sich selbst.
A = a · a
Beispiel 3
Ein Quadrat ist 5 dm lang.
Wie groß ist der Flächeninhalt?
Gesucht:
Flächeninhalt A
Gegeben:
a = 5 dm
Rechnung:
A = a · a
A = 5 · 5 dm2
A = 25 dm
Der Flächeninhalt beträgt 25 dm2.